String matching is a fundamental problem in computer science and has applications ranging from text processing to bioinformatics. The Rabin-Karp algorithm is one such approach to efficiently find a pattern within a larger text. This algorithm combines hashing and sliding window techniques to achieve linear-time average-case complexity. In this blog post, we’ll delve into the workings of the Rabin-Karp algorithm using a Java implementation.

Background

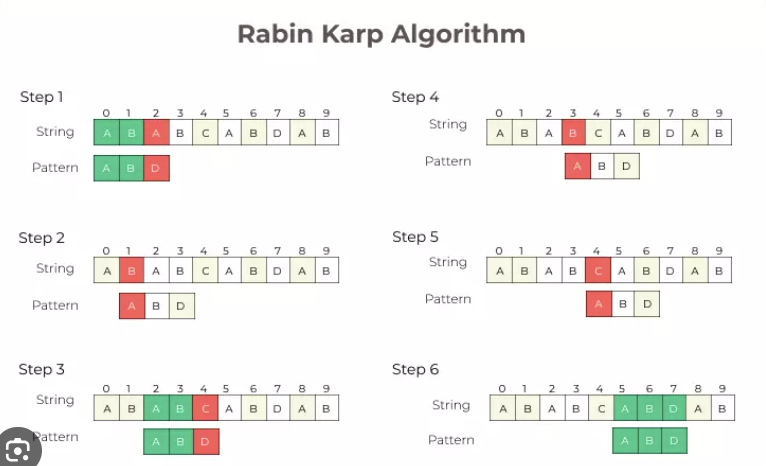
The Rabin-Karp algorithm is particularly useful for its ability to perform pattern matching in linear time on average. It achieves this efficiency by using a rolling hash function, which allows the hash value of a substring to be calculated in constant time. This is coupled with the observation that if two strings hash to the same value, they may be equal, enabling the algorithm to compare substrings quickly.

Key Components of the Algorithm

Let’s break down the key components of the Rabin-Karp algorithm using a Java implementation:

1. Hashing

private static int hash(String str, int length) {
    int hashValue = 0;
    for (int i = 0; i < length; i++) {
        hashValue += str.charAt(i) * Math.pow(PRIME, i);
    }
    return hashValue;
}

The hash function calculates the hash value of a given substring using a prime number (PRIME) as the base. The hash is computed by iterating through the characters of the substring and multiplying each character's ASCII value by an increasing power of the prime number.

2. Recalculating Hash

private static int recalculateHash(String text, int oldIndex, int patternLength, int oldHash) {
    int newHash = oldHash - text.charAt(oldIndex);
    newHash /= PRIME;
    newHash += text.charAt(oldIndex + patternLength) * Math.pow(PRIME, patternLength - 1);
    return newHash;
}
//Or

//alternative 
public double recalculateHash(double oldHash,char oldChar,char newchar,int patternLength){
        double hash=(oldHash-oldChar)/PRIME;
        hash+=newchar*Math.pow(PRIME,patternLength);
        return hash;
    }

The recalculateHash function is used to update the hash value efficiently when moving from one substring to the next. It subtracts the contribution of the character that is no longer in the substring, divides by the prime number, and adds the contribution of the new character at the end of the substring.

3. Checking Equality

private static boolean checkEquality(String pattern, String text, int startIndex) {
    for (int i = 0; i < pattern.length(); i++) {
        if (pattern.charAt(i) != text.charAt(startIndex + i)) {
            return false;
        }
    }
    return true;
}

The checkEquality function compares substrings character by character to ensure that a match is found.

4. Main Search Function

private static void search(String pattern, String text) {
    int patternLength = pattern.length();
    int textLength = text.length();
    int patternHash = hash(pattern, patternLength);
    int textHash = hash(text, patternLength);

    for (int i = 0; i <= textLength - patternLength; i++) {
        if (patternHash == textHash && checkEquality(pattern, text, i)) {
            System.out.println("Pattern found at index " + i);
        }        if (i < textLength - patternLength) {
            textHash = recalculateHash(text, i, patternLength, textHash);
        }
    }
}

The search function orchestrates the overall process. It calculates the initial hash values, iterates through the text, and efficiently updates the hash value for each substring, checking for equality and printing the indices where a match is found.

Example Run

Let’s consider an example to understand the algorithm better:

public static void main(String[] args) {
    String text = "ABABCABABABCABCABAB";
    String pattern = "ABABCABAB";
    search(pattern, text);
}

The output of this program would be:

Pattern found at index 0
Pattern found at index 1
Pattern found at index 8
Pattern found at index 15

public class RabinKarp {
    private final int  PRIME=101;
    public double calcHash(String str){
        double hash=0;
        for(int i=0;i<str.length();i++){
            hash+=str.charAt(i)*Math.pow(PRIME,i);
        }
        return hash;
    }
    public double strHash(double oldHash,char oldChar,char newchar,int patternLength){
        double hash=(oldHash-oldChar)/PRIME;
        hash+=newchar*Math.pow(PRIME,patternLength);
        return hash;
    }
    public void search(String str,String pattern){
        int patterLength=pattern.length();
        double strHash=calcHash(str);
        double patternHash=calcHash(pattern);
        for(int i=0;i<str.length()-pattern.length();i++){
            if(strHash==patternHash){
                if(str.substring(i,patterLength).equals(pattern)){
                    System.out.println("pattern at"+i);
                }
            }
            if(i<str.length()-pattern.length()){
                strHash=strHash(strHash,str.charAt(i),str.charAt(i+patterLength),patterLength);
            }
        }
    }
}

Conclusion

The Rabin-Karp algorithm provides an efficient way to search for a pattern in a given text. By leveraging hashing and the rolling hash technique, it achieves linear-time average-case complexity, making it a valuable tool for string matching applications. Understanding the key components of the algorithm and its implementation in a programming language like Java can deepen your appreciation for its simplicity and effectiveness.